
If f(x) is continuous function defined on.Some properties of definite integrals are: p(a) is antiderivative of f(x) at x = a.p(b) is antiderivative of f(x) at x = b, and.According to that, the formula for Definite Integral is: To calculate the definite integral of any function, we can use the Second Fundamental Theorem of Integral Calculus, which is already discussed above. The definite integral does not require any constant integration. The a and b are called the limits of integration where a is called the lower limit and b is called the upper limit of the integration. The interval is called interval of integration. It is denoted by f(x)dx and its value equals to p(b) – p(a) where p(b) is the antiderivative at x = b and p(a) is the antiderivative at x = a. The antiderivative p(x) of a continuous function f(x) on the interval is called a definite integral. The definite integrals are the integrals which are bounded by the limits. There are two types of integral: Definite integral and indefinite integral. The integral is the area under the curve. The integral is also called as the primitive function of f or Newton-Leibnitz integral. The reverse of differentiation is called as integration. The antiderivative of the function f is called the integral of f. The second fundamental theorem of integral calculus states that if f(x) is a continuous function on the interval and p(x) is the antiderivative of f(x), then f(x) dx = p(b) – p(a) where the integral is called as a definite integral and a and b are called as lower and upper limits of the integral respectively. Second Fundamental Theorem of Integral Calculus

The first fundamental theorem of integral calculus states that if P(x) = ∫ f(x) dx is a continuous function on the interval, then P'(x) = f(x) for all x ∈.

First Fundamental Theorem of Integral Calculus.There are two fundamental theorems of integral calculus: The integral represents the area under the curve. Fundamental Theorems of Integral Calculus There are various methods in Integral Calculus that are used in many ways such as to find the areas and volumes, approximate solutions of equations, calculate complex interactions of physical objects in our surroundings etc. This integral and integration hold many properties and the study of these properties in the branch of mathematics is called Integral Calculus.

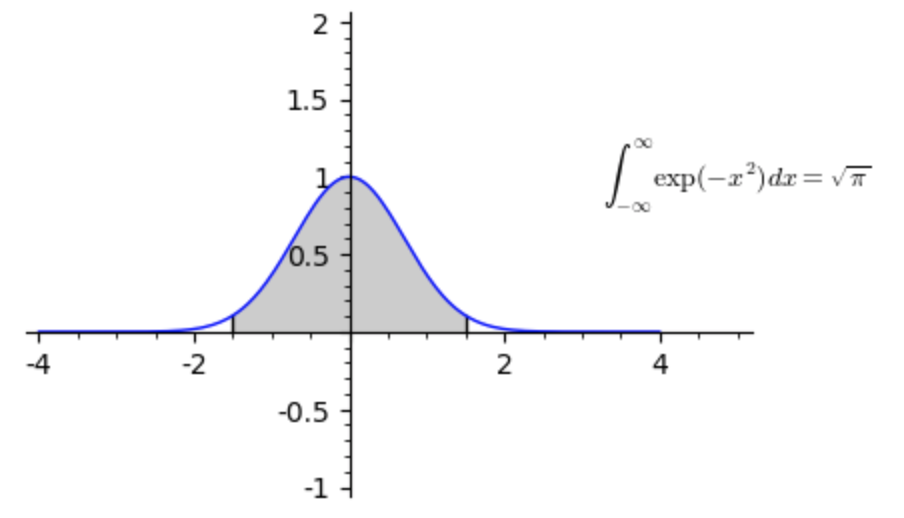
In this process, the result obtained after the integration is called the integral. The process of finding the function from its derivative is called anti-derivative which is also referred to as Integration. Fundamental Theorems of Integral Calculus.Role of Mahatma Gandhi in Freedom Struggle.


 0 kommentar(er)
0 kommentar(er)
